PRML復々習レーン
2.3.3
ガウス変数に対するベイズの定理

tomerun

やること

2.3.1節・2.3.2節では、ガウス分布に従うベクトル変数xの次元を 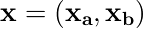と2つに分割し、次を求めた。

• 一方をfixしたときのもう一方の条件付き分布
• 一方を周辺化した周辺分布

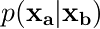
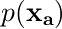
条件付き分布 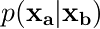は、固定した方の要素 x_b についての線形関数になっていた。 (式 2.97)

→逆（？）に、あるガウス分布に従う変数 x があったとき、平均が x の線形関数になる条件付きガウス分布 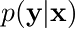を考え、その周辺分布などを見てみる

これ、あとの章で頻繁に出てくるそうですよ

準備

もともとある分布

平均がこの変数 x の線形関数になる、条件付きガウス分布

2つの変数をまとめて扱う記法

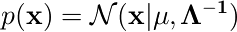
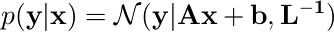
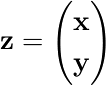
yの周辺分布 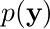と、yが与えられた下でのxの条件付き分布 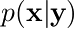はどうなるか？

※ x と y の次元は等しいとは限らないことに注意

同時分布

まず同時分布について

これまでの節でもやってたように、指数の肩の部分を2次式として見る。確率の対数を取ることで指数の肩のみを扱う

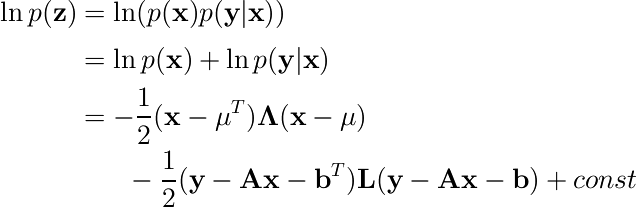
→これは x と y の2次式なので、この x と y の同時確率もガウス分布

同時分布の共分散行列

x と y の2次の項を整理すると

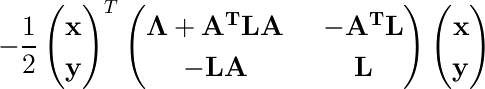
これを式2.71と見比べて、精度行列 R は次のようになる

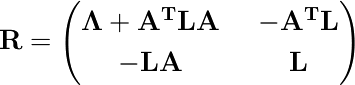
逆行列の公式2.76を使って計算すると、共分散行列が求められる

同時分布の平均(1)

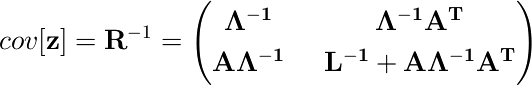
次に、x と y の1次の項を整理すると

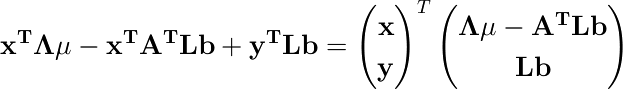
ここで、Λ や L は共分散行列なので対称行列だから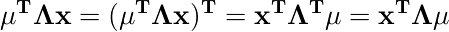

などとなることを利用している。

これをまた式2.71と見比べると、

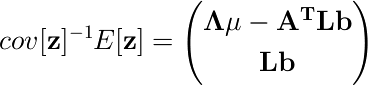
なので

同時分布の平均(2)

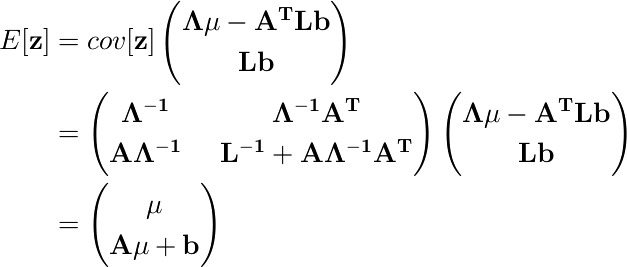
ということで、同時分布の共分散行列と平均が求められた。

周辺分布

次に x を周辺化した y の周辺分布を求めるが、これは今得た同時分布と2.3.2でやったこと（同時分布が与えられ、一部の変数集合についての周辺分布を求める）を使えばすぐわかる。

式（2.92）、(2.93)にあるように、周辺分布の平均と共分散は、同時分布の分割した平均と共分散から得られる。

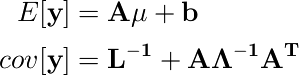
※2.3.2でいう x_a = ここでの y
※2.3.2節とこの節では考えている対象の要素の位置が上下入れ替わっていることに気をつける。

条件付き分布

2.3.1の結果を使うと、条件付き分布 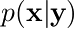の平均と共分散もすぐわかる。

まず、式（2.73）から

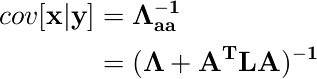
であり、式（2.75）から

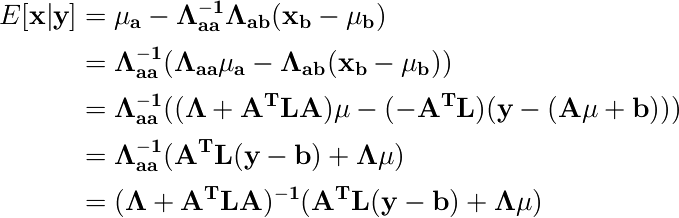
となる。

ベイズの定理としての解釈

分布 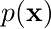を x の事前分布と見なす。

観測値 y を得た後で得られる条件付き分布 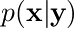を、 x の事後分布として使える。

これはガウス変数に対してのベイズの定理