PRML復々習レーン
4.3.3
反復再重み付け最小二乗
4.3.4
多クラスロジスティック回帰
tomerun
PRML復々習レーン
やること
ロジスティック回帰の識別モデルとしての最尤解を（解析的には無理だから近似的に）求めよう！！
使う手法
ニュートン-ラフソン法を使う。いわゆるニュートン法
誤差関数 E(w) を最小化するには、Eの一階微分の零点をニュートン法を用いて求める。
具体的には、次の式でパラメタwを更新する
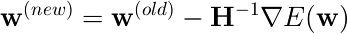
ここで、HはEのヘッセ行列
二乗和誤差関数の場合:練習として(1)
ひとまずロジスティックとかは置いておいて、確認のため二乗和誤差関数（3.1.1節）についてニュートン法を適用してみる。
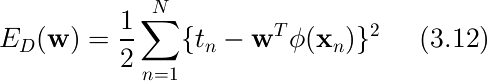
から、微分すると
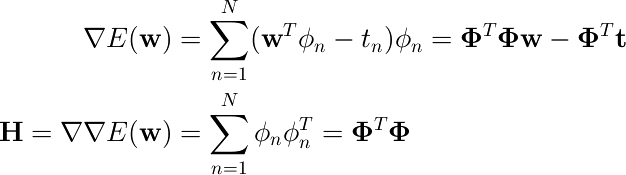
Φは、n行目が入力ベクトル φnT で与えられる N×M 行列
二乗和誤差関数の場合:練習として(2)
これをニュートン法の式に入れて計算すると、
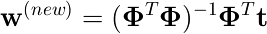
となる。
w(old)は消え、Eの最小値を与えるwが閉じた形で求まった。これは3.1.1節での結果と一致している。
※ニュートン法は、目的関数を1次近似することで近似解を求める手法だということを考えると、ここでのニュートン法の目的関数であるEの一階微分がwの一次式なので、このように厳密解が出てくるという結果は納得できる。
2クラスロジスティック回帰の場合(1)
2クラスのロジスティック回帰では、前の節の結果(4.91)から、誤差関数の微分は次のようになる。
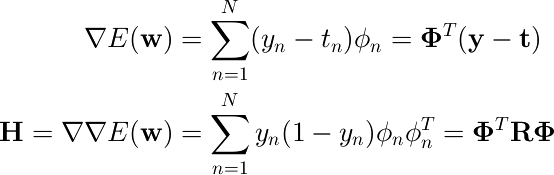
Rは対角行列であり、その対角要素は次で与えられる。
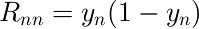
ヘッセ行列Hが正定値行列である（演習4.15、アンチョコ本参照）ので、Eは凸関数であって最小値を持つ。ということでニュートン法を適用できる。
2クラスロジスティック回帰の場合(2)
をニュートン法の式に入れて計算すると、
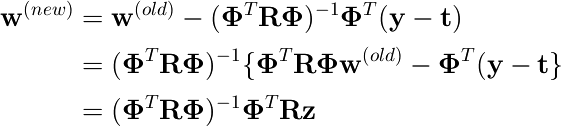
ここで、zは次で与えられる。
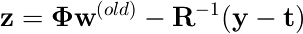
これは重み付き最小二乗法の正規方程式と同じ形。
ただし、重み行列Rがwに依存しているので、これは閉じた解ではない。繰り返しこの方程式を計算して近似解を求める必要がある
この手法を反復重み付き最小二乗法（IRLS）と呼ぶ。
IRLSの解釈
目的変数tの分散を計算すると、
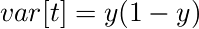
となって、重み付け行列の要素に一致する。ということで、重み付け行列 R は分散として解釈できる。
また z については、次のようにロジスティックシグモイド関数を1次近似した空間での目的変数値と一致する。
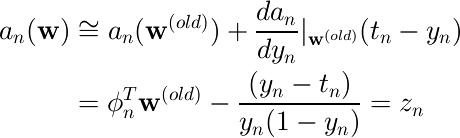
（ここ、いまひとつ意味がつかめていないので補足できる方はお願いします）
多クラスロジスティック回帰の場合(1)
多クラスの分布では、事後確率はソフトマックス関数で表される。
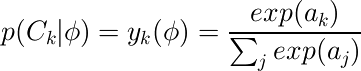
ここで、aは次で表される。
目的変数は1-of-K表記法で表現することにする。
すなわち、特徴ベクトルφnがクラスkに属するとき、目的変数ベクトルtnはk番目の要素が1でそれ以外は0
多クラスロジスティック回帰の場合(2)
尤度関数は次のようになる。
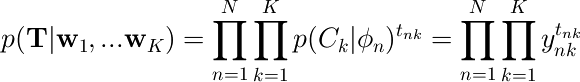
ここで、T はtnkを要素とする N×K 行列
いつものように尤度関数の負の対数を取ると、
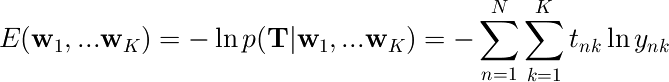
このEを交差エントロピー誤差関数と呼ぶ。
多クラスロジスティック回帰の場合(3)
Eをパラメータベクトル wj で微分すると次のようになる。
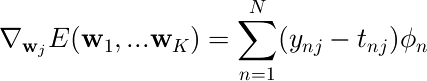
計算の過程で、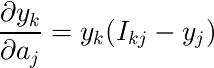 
と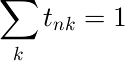 
の関係を使った。
この、誤差 (ynj - tnj) と基底関数φnとの積という形は、以前（(4.96)、(3.13))にも現れている。これはより一般的な結果であることを後の節で見る。
多クラスロジスティック回帰の場合(4)
Eのヘッセ行列は、M×MサイズのブロックがK×K個存在するMK×MK行列になる。
(j,k)番目のブロックは次のようになる。
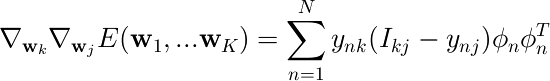
このヘッセ行列は正定値である（演習4.20、アンチョコ本参照）。
よって、これをもとに、多クラスのロジスティック回帰でも識別パラメータをニュートン法により計算できる。