PRML復々習レーン

5.5.3-5.5.5
ニューラルネットワークの不変性

tomerun

宣伝

来週、Advent Calendarの記事を書きます。

• Competitive Programming Advent Calendar
• 『Kaggleについて』
• http://topcoder.g.hatena.ne.jp/tomerun/20121221 （予定）
• Machine Learning Advent Calendar
• 『機械学習で文字コードの自動判別をやってみる』
• http://d.hatena.ne.jp/tomerun/20121222 （予定）

お楽しみに

やること

パターン認識では入力に対する不変性が要請されることが多いので、ニューラルネットワークではそれをどう扱うか見ていく。

不変性とは

分類問題において、入力に対して小さな変換を行っても、出力されるクラスは変化しない

変換の例：平行移動・回転・拡大縮小・色の変化・ピクセル欠損・図5.14のようなグニャグニャした移動

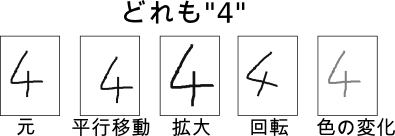
訓練データの数がめちゃめちゃ多かったら自然と不変性を学習してくれるのだろうが、普通そんなことはないので何らかのアプローチで不変性を取り込む

→汎化性能の向上を期待

不変性を取り扱う

2つめの手法のひとつである接線伝播法についてこれから説明する。

接線伝播法

やることは、誤差関数Eに不変性の保たれなさのペナルティを付け足して、誤差関数をグレードアップさせること。

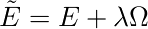
ここでΩは正則化関数であり、不変性の破れについてのペナルティを表す。

簡単のため、入力x_nに対する変換が1つのパラメタξで表されるとする。

Ωを例えば次のようにすると、入力の変換に対して出力が変化しない場合、この項が0に近づき誤差関数が小さくなる。

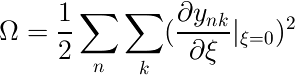
※y_nkは、n個目のデータ点でのk番目の出力

接線伝播法

yのξに関する微分は次のように計算できる。

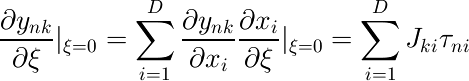
J_kiはヤコビ行列の要素であり、ニューラルネットワーク上の逆伝播によって計算できる。（→5.3.4）

τ_niは、n番目のデータ点の入力についての、ξに関する接線のi次元目の要素である。

この値は、実際に入力を微小変化させることで計算できる。（→図5.16：何をやっているのかよくわからない…）

接線伝播法

Ωのネットワーク重みについての微分は、逆伝播によって計算できる。（→演習5.26）

変換が1つのパラメタで表せない場合も、今見たΩと同じ形の項を各パラメタについて足し合わせれば良い。

この接線伝播法の他にも、接距離（tangent distance）という方法がある。
詳細は論文に http://home.mit.bme.hu/~gtakacs/download/simard1998.pdf

接線伝播法と変換データでの訓練

さきほど見た対称性を扱うアプローチの中に、「データ点を自分で変換して増やしてやる」という方法があったが、実はこれと接線伝播法には関係がある。

入力の変換が1つのパラメタξで表現できるとして、入力xに対して変換を行って得られるベクトルをs(x,ξ)と表す。※s(x,0)==x

データ数無限の極限では、二乗和誤差関数は次のように書ける。

接線伝播法と変換データでの訓練

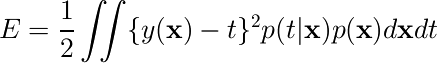
各データ点に対してデータを無限個コピーして、それぞれが確率分布p(ξ)で定まる変換を受けているとすると、二乗和誤差関数は次のようになる。

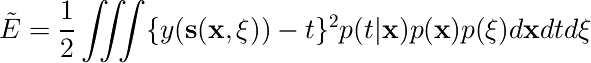
小さい変換だけを考えるので、変換された入力に対する出力 y(s(x,ξ)) をxのまわりでテイラー展開すると、

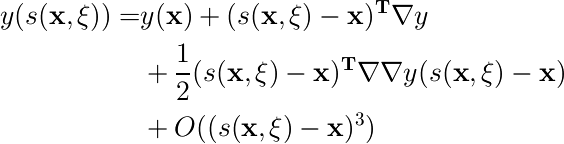
（sはベクトルなのでO((...)^3)は正確な記法ではないが）

接線伝播法と変換データでの訓練

また、s(x,ξ)をxのまわりでテイラー展開すると、

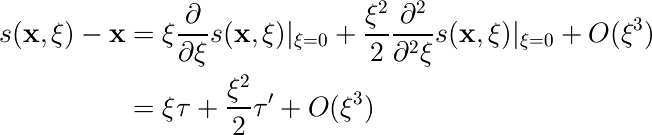
これを先ほどのyの式に使うと、次のようにまとめられる。

接線伝播法と変換データでの訓練

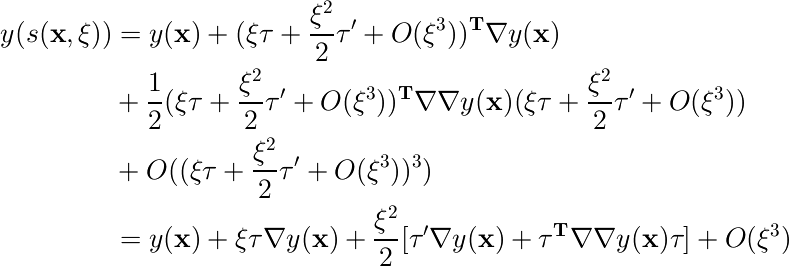
これを誤差関数に代入してまとめると、次のようになる。

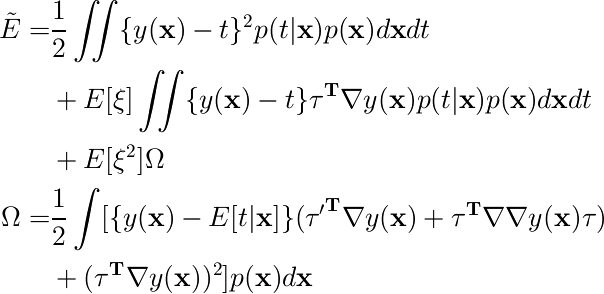
さまざまな微少変換を偏りなく考える場合、変換のパラメタξの平均E[ξ]は0になる。また、もとの誤差関数をEで、E[ξ²]をλで表し、O(ξ³)の項を無視すると

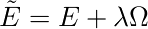　接線伝播法でやったのと同じ形

接線伝播法と変換データでの訓練

正則化項のΩを簡単に表そう。

これまでの章の議論から、もとの誤差関数Eを最小化するyは 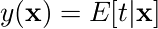であることが分かっている。

正則化項はO(ξ²)なので、正則化誤差全体を最小化するyは 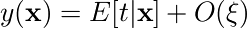の形になる（？？？）。

したがって、Ωの第一項はO(ξ)で、正則化誤差全体に与える影響はO(ξ³)となって無視される。

すると、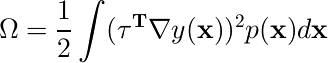 と簡単な形になる。

これは、「(入力の変換パラメタに対する微分*出力の入力に対する微分)²の和」 という形であり、接線伝播法で作った正則化項と同等。

接線伝播法と変換データでの訓練

変換が 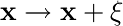という単なるランダムノイズの付加だった場合、正則化項は次の形になる。

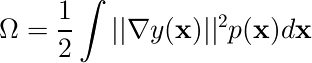（Tikhonovの正則化）

注意：これまでパラメタξは一次元だったが、ここではしれっとξが多次元になっている（入力xをD次元とするとξもD次元）。τは行列になるので前ページの結果をそのまま適用できない。計算の詳細は演習の回答を参照